The key feature of the BIGNUM arithmetic is the following one:
that calculations are performed on numbers which digits of precision are limited only by the available memory of the host system.
Several languages have builtin support for bignum, here you are a non complete list:
- Common Lisp
- C#: System.Numerics.BigInteger
- ColdFusion
- D: standard library module std.bigint
- Dart: the built-in int datatype implements arbitrary-precision arithmetic
- Erlang: the built-in Integer datatype implements arbitrary-precision arithmetic.
- Go: the standard library package big implements arbitrary-precision integers (Int type) and rational numbers (Rat type)
- Haskell: the built-in Integer datatype implements arbitrary-precision arithmetic and the standard Data.Ratio module implements rational numbers.
- Java: class java.math.BigInteger (integer), Class java.math.BigDecimal (decimal)
- Perl: The bignum and bigrat pragmas provide BigNum and BigRational support for Perl.
- Python: the built-in int (3.x) / long (2.x) integer type is of arbitrary precision. The Decimal class in the standard library module decimal has user definable precision.
- Ruby: the built-in Bignum integer type is of arbitrary precision. The BigDecimal class in the standard library module bigdecimal has user definable precision.
- Standard ML: The optional built-in IntInf structure implements the INTEGER signature and supports arbitrary-precision integers.
Common use of arbitrary-precision arithmetic
A common application is public-key cryptography (such as that in every modern Web browser), whose algorithms commonly employ arithmetic with integers having hundreds of digits.
Arbitrary-precision arithmetic can also be used to avoid overflow, which is an inherent limitation of fixed-precision arithmetic.
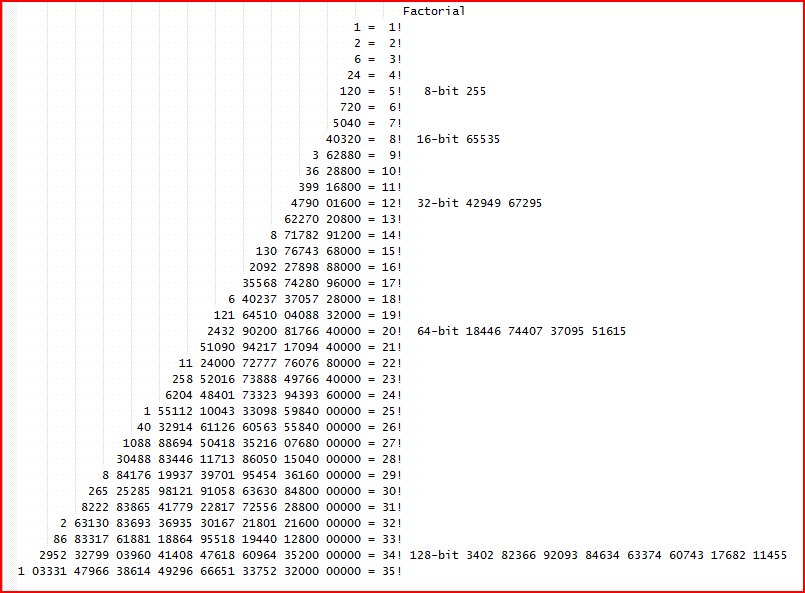
Another use is the computation of the factorial numbers.
Implementation
Arbitrary-precision arithmetic is considerably slower than arithmetic using numbers that fit entirely within processor registers, since the latter are usually implemented in hardware arithmetic whereas the former must be implemented in software.